Když programujeme nějakou hru, očekáváme, že objekty v naší 3D scéně budou správně vykresleny. Nastavíme si parametry kamery (projekční matici a matici pohledu), rozmístíme si modely na správná místa a už se těšíme, jak náš panáček bude stát před svým domkem a za celou scénou bude v pozadí silueta hor. Pro neprůhledné objekty to v XNA Frameworku bude fungovat přesně tak, jak čekáme, nebudeme se muset o nic víc starat.
O správné pořadí objektů se zde automaticky stará Depth Buffer. Ten si udržuje pro každý pixel obrazovky blízkost nejbližšího dosud vykresleného objektu. Pokud chceme následně vykreslit další objekt, porovná se jeho vzdálenost od kamery s informacemi v tomto bufferu a buď se vykreslí celý, jenom jeho část, nebo se nevykreslí vůbec.
Tento přístup ale nebude fungovat v případě, že bychom chtěli mít ve scéně nějaké poloprůhledné objekty. Pokud bychom nejdříve vykreslili vzdálenější objekt a potom ten bližší, vše by bylo v pořádku. Pokud bychom ale pořadí prohodili, zadní objekt by nám nepříjemně vystoupil dopředu (průhlednost se nedá takhle sčítat). Tuto chybu můžeme jednoduše poznat, pokud si umístíme dva modely vedle sebe, vykreslíme je s nastavením device.BlendState = BlendState.AlphaBlend; (notace z XNA 4.0) a ve standardním vykreslovacím cyklu jim pro každý mesh nastavíme effect.Alpha = 0.8f; Když potom budeme zkoušet otáčet kamerou okolo těchto objektů, z jedné strany budou zobrazeny správně, ale z druhé špatně.
Pokud tedy opravdu budeme chtít v naší hře vidět skrz některé objekty, budeme si je muset před vykreslením každého snímku nějakým způsobem seřadit vůči kameře, směrem od nejvzdálenějšího k nejbližšímu.


Jaká tedy bude naše základní idea?
- Zkontrolujeme, že je nastaveno device.DepthStencilState = DepthStencilState.Default; (notace z XNA 4.0, ve starších verzích tomu odpovídá nastavení DepthBufferEnable a DepthBufferWriteEnable na true)
- Vykreslíme všechny neprůhledné objekty
- Přepneme device.DepthStencilState = DepthStencilState.DepthRead; (ve starších verzích tomu odpovídá nastavení DepthBufferWriteEnable na false)
- Setřídíme poloprůhledné objekty vůči kameře od nejvzdálenějšího k nejbližšímu a vykreslíme je takto odzadu
- Přepneme zpátky na device.DepthStencilState = DepthStencilState.Default;
Hned na začátku si musíme dát nějaká omezení, se kterými budeme muset počítat. Je pravda, že správné pořadí vykreslování nelze určit vždy. Například kuličku umístěnou do skleničky se nám nikdy nepodaří seřadit tak, aby byla správně umístěna vůči jejím oběma stěnám. Stejně tak, pokud nám budou pronikat dva objekty skrz sebe, nepůjde to takhle jednoduše. Na to potom existují další rozšíření algoritmů, kdy se navzájem posuzují jednotlivé polygony modelů a v případě problému se dále rozdělují. Pokud ale chceme programovat hru, nebo rychle vykreslovat nějakou obecnou 3D scénu, záleží nám hlavně na výkonu. Případné problémy, které by mohly nastat, můžeme ošetřit jiným poskládáním herního levelu, nebo úplným zanedbáním průhlednosti.
Je zajímavé, že i když si problém zobecníme natolik, že naše herní modely budou uzavřené do neprotínajících se kvádrů (bounding boxů), které navíc budou na sebe rovnoběžné a kolmé, pořád nebudeme mít vyhráno. Již u čtyř objektů může nastat situace, kterou prostým seřazením nebudeme schopni vyřešit, viz obrázek. Který objekt by měl být vykreslen první? Jaký tedy zvolíme kompromis?

V návrhu našeho algoritmu vyjdeme z takzvaného Malířova algoritmu (nebo také algoritmu Newell Newell Sancha, publikovaného v roce 1972). Ten se zabývá řazením jednotlivých polygonů, je zde podán návod i na to, jak by se měly v případě problémů dále dělit.
My budeme chtít řadit vůči sobě celé objekty. Každý budeme posuzovat podle jeho “orientovaného bounding boxu”, nejmenšího natočeného kvádru, do kterého se vejde celý objekt. Ten si můžeme představit jako osm bodů odvozených z minima a maxima původního bounding boxu, na které se provedla transformace objektu (to skutečné napozicování do herního levelu – pootočení, zvětšení a posun).
Objekty budou moci být obecně umístěné a natočené, tyto jejich orientované bounding boxy by se ale neměly protínat. Situaci budeme posuzovat ve výsledných transformovaných souřadnicích obrazovky, neboli, že objekt nejvíce nalevo/nahoře bude mít nejmenší hodnotu x/y, tak, jako by to bylo 2D. Na ose z budeme mít “vzdálenost od obrazovky”. Přepočet bodů do těchto souřadnic získáme, pokud je vynásobíme projekční maticí a maticí pohledu.
Když k bodu přidáme čtvrtou souřadnici w nastavenou na 1, následně ho ztransformujeme a body x/y/z touto převedenou souřadnicí w vydělíme, dostaneme pozici na obrazovce v rozsahu x/y od –1 do 1. Souřadnice z bude od 1 (bod v “nekonečnu”) do 0 (bod na ořezové rovině kamery).
Pěkné vysvětlení, jak ve 3D grafice funguje toto převádění souřadnic je v tomto článku. Přikládám ale i malý kousek pseudokódu. Pro originální bounding box objektu najde pozice osmi transformovaných bodů:
Matrix transformMatrix = worldMatrix * camera.ViewMatrix * camera.ProjectionMatrix;
for (int i = 0; i < objects.Count; i++)
{
Vector3 min = objects[i].OriginalBoundingBox.Min;
Vector3 max = objects[i].OriginalBoundingBox.Max;
bbPoints[0] = new Vector3(min.X, max.Y, min.Z);
bbPoints[1] = new Vector3(max.X, max.Y, min.Z);
//...
for (int j = 0; j < 8; j++)
{
// Provede transformaci bodů bounding boxu na orientovaný bounding box
bbPoints[j] = Vector3.Transform(bbPoints[j], objects[i].Transforms);
// Převede body do 2D souřadnic obrazovky
bbPoints4[j] = new Vector4(bbPoints[j], 1);
bbPoints4[j] = Vector4.Transform(bbPoints4[j], transformMatrix);
// Vydělí "w", x/y bude od -1f do 1f; z = 1f (vzdálený bod), z = 0f (bod na ořezové ploše kamery)
boxes[i].ScreenXYZ[j] = new Vector3(bbPoints4[j].X / bbPoints4[j].W, bbPoints4[j].Y / bbPoints4[j].W, bbPoints4[j].Z / bbPoints4[j].W);
}
}
Já jsem si k tomu ještě na konci převrátil hodnoty na ose z, aby byly od –1 do 0 a více odpovídaly běžnému zobrazování souřadnic. Dále jsem si udržoval naalokované pole o velikosti počtu poloprůhledných prvků. Do něj jsem si ukládal objekty udržující si odkaz na konkrétní model k vykreslení a pamatující si minimální a maximální souřadnici x/y/z a spočítané body přetransformovaného bounding boxu do souřadnic obrazovky.
Nyní se už konečně můžeme pustit do toho, jak poběží náš algoritmus: Objekty si seřadíme podle nejvzdálenější souřadnice z. Vezmeme nejvzdálenější box (označíme b1) a budeme ho postupně testovat proti všem bližším (b2), postupně všemi podmínkami. Pokud se nám jakákoliv podmínka potvrdí, znamená to, že vůči tomuto boxu je pořadí správné (buď je opravdu b1 za b2, nebo na pořadí nezáleží). Pokud se potvrdí některá z podmínek vůči všem bližším boxům, znamená to, že objekt můžeme bez obav vykreslit a nemusíme se jím dále zabývat.
Pokud vůči nějakému boxu b2 selžou všechny podmínky, zkusíme s tím něco udělat. Box b2 přesuneme na začátek, ostatní prvky posuneme (já jsem si například v poli boxů udělal spojový seznam a jen jimpopřepojoval odkazy). Také ho označíme, jako že byl už jednou přesouvaný. Pokud na něj narazíme ještě jednou a měli bychom ho znovu přesouvat na začátek, rovnou ho pošleme na výstup k vykreslení. Tuto situaci bychom nedokázali jinak vyřešit.
Budeme postupně ověřovat tyto podmínky, od nejjednodušších k výpočetně náročnějším:
- Nejvzdálenější souřadnice b2.z je blíž, než nejbližší b1.z (posuzujeme podle zapamatovaných min/max)
- b1 a b2 se neprotínají v ose x
- b1 a b2 se neprotínají v ose y
- Celý box b1 je za boxem b2
- Celý box b2 je před boxem b1
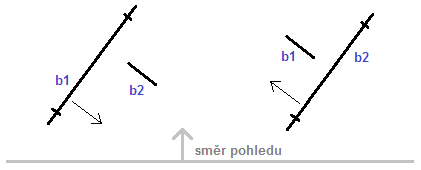
Čtvrtá a pátá podmínka vypadají podobně, ale pro správnou funkčnost je musíme ověřit obě. Obrázek napoví, proč by to mělo být potřeba. Uvažujeme pohled shora na dvě úsečky a předpokládáme, že b1 je za b2:
Ve čtvrté a páté podmínce se skrývá ještě jedna záludnost. Ve standardním Malířově algoritmu se počítá s polygony, my jsme si ho ale zobecnili na orientované bounding boxy. Jak z toho ven? Ukažme si to například na čtvrté podmínce, pátou ošetříme obdobně:
Náš transformovaný bounding box si můžeme rozložit na osm polygonů, podobně jako kdybychom si rozkládali krychli na čtvercové stěny. Protože uvažujeme v převedených souřadnicích, pozice bodů se nám budou překrývat stejně, jako na obrazovce. Můžeme tedy z toho poznat, zda je daná strana přivrácená nebo odvrácená!
Dosadíme si tři body stěny a vektorovým součinem spočítáme normálový vektor. Pokud jeho souřadnice z bude záporná, směr strany míří směrem od nás a je to odvrácená strana. Tento test bude správně fungovat v jakékoliv projekci, perspektivní i ortografické (protože už počítáme ve výsledných souřadnicích). Většinou budeme mít, podle pohledu kamery, jednu až tři strany přivrácené, zbytek odvrácených.
Nyní si spočítáme rovnici roviny této stěny (dosazením bodu x/y/z do výrazu Ax+By+Cz+D; bod D získáme dosazením normálového vektoru a jednoho bodu roviny). Pokud tam nyní dosadíme postupně všechny body druhého boxu a pokaždé vyjde >0, znamená to, že se celý druhý box nachází za nějakou zadní stěnou prvního boxu. Stačí ověřit, že toto platí pro jednu jedinou jeho zadní stěnu. Protože zde ještě mohou nastat zaokrouhlovací problémy u přilehlých stěn, můžeme například v rovnici porovnávat, jestli je výraz větší, než -0.000001f.
