V minulém díle jsme se naučili základní algoritmy pro třídění dat. Dnes si ukážeme algoritmus MergeSort. Ještě než se k němu dostaneme, máme tady jednu úlohu, která se nám bude velice hodit.
Sloučení setříděných posloupností
Představte si, že máte dvě setříděná pole čísel. Potřebujeme tato čísla slít do jednoho pole tak, aby bylo setříděné. Jak tato dvě pole slít do jednoho?
Na začátku si vytvoříme dvě proměnné, například k a l a nastavíme jim jako hodnotu 0. Tyto proměnné nám budou ukazovat do polí A, resp. B, a budou říkat, který prvek máme dále zpracovávat. Také budeme mít proměnnou j, která nám bude říkat, kolik prvků jsme již zapsali do pole C, kde chceme mít výsledek. Také ji ze začátku nastavíme na nulu.
Nyní se v každém kroku algoritmu podíváme, ve kterém z polí A nebo B je menší číslo (na pozicích, kam ukazují proměnné k a l). Vybereme tu menší, opíšeme ji do pole C (na pozici j) a přičteme k j jedničku, abychom věděli, kolik prvků už máme zapsaných. A protože jsme číslo, které jsme vybrali, už zpracovali, zvětšíme o jedničku buď k nebo l podle toho, ze kterého pole jsme jej vzali.
A to se celé opakuje, dokud nezpracujeme všechna čísla. Opět se podíváme do pole A na pozici k a do pole B na pozici l, vybereme menší číslo, přepíšeme jej do výsledného pole C a zvětšíme o jedničku k nebo l podle toho, odkud jsme číslo vzali.
Jediné, co zbývá pohlídat, je případ, kdy z jednoho nebo druhého pole už zpracujeme všechna čísla. Pak je potřeba zbytek toho druhého pole přepsat do pole C a hlavně hlídat, abychom při porovnávání čísel nesahali mimo pole.
Vše je vidět na animaci (musíte mít nainstalován doplněk Microsoft Silverlight):
Bylo by velmi dobré, kdybyste si tento program zkusili napsat opravdu sami bez pomoci, najít v něm všechny chyby a ošetřit to tak, aby vše fungovalo.
Jako pole A a B použijte například tyto:
Dim A() As Integer = {12, 15, 20, 34, 75}
Dim B() As Integer = {-2, 5, 21, 24, 27, 34, 35, 36}
Váš program by měl vytvořit pole C potřebné délky (délky polí zjistíme pomocí A.Length a B.Length) a naplnit ho setříděnými hodnotami z polí A a B. Důležité je, abyste použili tento postup, nebylo by k ničemu zkopírovat hodnoty do pole C tak, jak jsou, a pustit na to algoritmus z minula (i když fungovalo by to také).
Pokud nevíte jak, zkuste si přečíst tento článek ještě jednou od začátku a zkusit přemýšlet, pokud stále nevíte, zde je příklad, jak by to mělo vypadat (možností je samozřejmě více):
Dim A() As Integer = {12, 15, 20, 34, 75}
Dim B() As Integer = {-2, 5, 21, 24, 27, 34, 35, 36}
Sub Main()
Dim k As Integer = 0 'ukazatel v poli A
Dim l As Integer = 0 'ukazatel v poli B
Dim C(A.Length + B.Length - 1) As Integer 'výstupní pole
While k < A.Length Or l < B.Length 'opakovat, dokud oba ukazatele nedojely na konec pole
Dim vybrat As Integer
If k = A.Length Then 'už jsme došli na konec prvního pole, takže můžeme tahat jen z druhého
vybrat = 2
ElseIf l = B.Length Then 'už jsme došli na konec druhého pole, takže můžeme tahat jen z prvního
vybrat = 1
Else 'porovnat oba prvky a vybrat menší
If A(k) < B(l) Then vybrat = 1 Else vybrat = 2
End If
'opsat vybraný prvek do výstupního pole
If vybrat = 1 Then
C(k + l) = A(k)
k += 1
Else
C(k + l) = B(l)
l += 1
End If
End While
'vypsat pole
For i As Integer = 0 To C.Length - 1
Console.Write(C(i) & " ")
Next
Console.ReadKey()
End Sub
Program by se dal jistě napsat lépe a elegantněji, ale tady je hlavně důležité, aby bylo naprosto jasné, co která část dělá, a jak to přesně funguje. Vnější cyklus While pracuje, dokud ukazatele k a l ještě nedojely na konec pole (alespoň jeden z nich má hodnotu menší než délka pole, tzn. ukazuje ještě na nějakou buňku). Do proměnné vybrat si uložíme jedničku nebo dvojku podle toho, ze kterého pole na konci prvek opíšeme na výstup.
Pokud jsme už došli na konec prvního pole, musíme zbylé prvky opisovat z pole B, analogicky pokud jsme došli na konec druhého pole, budeme opisovat z pole A. Obě podmínky zároveň platit nemohou, to kontrolujeme ve While cyklu, který by nás už dovnitř nepustil. Pokud nejsme na konci ani v jednom poli, pak proměnnou vybrat stanovíme podle toho, ve kterém poli je menší číslo.
Pak už jenom proměnnou vybrat otestujeme a podle toho, co v ní je, opíšeme do pole C na pozici k + l číslo z příslušného pole. A posuneme také ukazatel na další políčko, abychom ho už nezpracovávali znovu. Tady je jedna finta - do pole C totiž zapisujeme na pozici k + l. Na začátku jsou v obou proměnných nuly a v každém kroku jednu z nich o jedničku zvýšíme. To znemená, že v prvním kroku bude tento součet roven nule, ve druhém jedné, ve třetím dvěma atd. Mohli bychom si místo toho udělat proměnnou m a tu v každém kroku zvětšit o jedničku, ale tohle je hezké na přemýšlení.
Poznámka: Tento algoritmus funguje pouze pokud víme, že pole A a B jsou setříděná. Jinak je k ničemu.
Třídící algoritmus MergeSort
Asi si říkáte, k čemu jsme psali tuhle opičárnu pro spojení dvou setříděných polí. Zbytečné to nebylo, je to pravděpodobně nejdůležitější část třídícího algoritmu MergeSort (třídění sléváním). Jak tento algoritmus funguje?
Inu, není na tom nic složitého. Na vstupu dostane pole čísel, to rozdělí na dvě poloviny, ty setřídí, a pak je právě tou naší opičárnou slije do jednoho setříděného pole. Kdekdo by řekl, že se to dalo čekat, ale zásadní problém je v tom, jak setřídí ty dvě půlky?
Zásadní vlastností programátorů je to, že se nezastavíme před ničím. Na setřídění obou polovin použijeme totiž algoritmus MergeSort. Co on totiž dělá? Dostane pole čísel, nějak ho setřídí a vrátí nám ho setříděné. Když mu tedy nejdřív dáme první polovinu původního pole, něco s ní udělá, a vrátí ji seřazenou. To samé provede s druhou polovinou, a opět nám ji vrátí seřazenou. Tyto dvě seřazené půlky už umíme spojit.
Někomu už možná došlo, že budeme používat rekurzi. Rekurze je speciální programovací technika, při které voláme funkci, ve které právě jsme. Chvíli trvá, než se do toho člověk dostane a pochopí ji, ale pro správného programátora je velmi důležitá. My si rekurzi pokusíme vysvětlit právě na algoritmu MergeSort.
Pohádka o rekurzi a MergeSortu
Bylo nebylo, král měl pole čísel a chtěl je setřídit. No dobře, nemůže mít pole čísel, tak má třeba meče různé velikosti a chce je na stole srovnat podle velikosti. Komu řekne? No přece princi, ten se určitě ve zbraních vyzná. A krom toho aspoň jednou za čas udělá něco užitečného.
Princ tedy dostane jeden velký stůl plný mečů, které má setřídit. Jenže princ se přece nebude zahazovat takovou prací, takže si zavolá dva sluhy, meče rozdělí na poloviny, a každý sluha dostane za úkol svoji polovinu seřadit. Až to budou mít, princ už tyto dvě setříděné poloviny nějak dotřídí.
Sluhové jsou velmi pracovití, ale mají jiné starosti s princeznou, která si pořád vymýšlí, a tak každý sluha požádá o pomoc dvě komorné, opět jim svoje díly rozdělí na půlky a až to komorné budou mít hotové, sluhové to spojí dohromady.
Komorné jsou ale rády, když meče vůbec uzvednou, a tak každá opět požádá dva kováře z města, kteří opět dostanou polovinu jejich práce a mají meče seřadit.
Co se s tím ale kovář bude párat, má přece u sebe pár pomocníků, takže opět práci rozdělí na půl, a hle, každý pomocník už má na setřídění jenom dva nebo jeden.
Protože pomocníky nikdo neposlouchá a kdyby po někom něco chtěli, tak by je ten někdo asi kopnul, musí tu špinavou práci udělat sami. Vezmou tedy své dva meče a srovnají je podle velikosti. Pak jdou za kovářem. Ten meče od obou učedníků srovná dohromady a donese to komorné. Ta opět meče od dvou kovářů s jejich laskavou pomocí dotřídí, pak zavolá sluhu, ten opět spojí dohromady dvě hromady mečů tak, aby byly podle velikosti. Za chvíli už má princ obě dvě poloviny setříděné, takže už zbývá je jenom srovnat dohromady.
No, když večer král přišel ujistit se, že se princ zase neopil a nerozbil kdeco, užasl. Uviděl srovnaný plný stůl mečů a všechny bylo správně seřazené podle velikosti. Pochválil prince a celé království žilo šťastně až do smrti.
A jak tedy MergeSort napsat?
Kdybyste chtěli naprogramovat tuto pohádku, asi by bylo dobré napsat procedury Princ, Sluha, Komorná, Kovář a Pomocník. Pokud byste je opravdu napsali, zjistíte ale, že procedury Princ, Sluha, Komorná a Kovář jsou de facto stejné. V každé pouze rozdělíme práci na polovinu, předáme ji někomu jinému, a až odstaneme oba výsledky, spojíme je dohromady. Pomocník dělá něco trochu jiného, ale s pomocí podmínky by se i tohle dalo dát do jedné procedury.
Uznávám, že pohádka asi nebyla nic moc, ale doufám, že demonstrovala, jak MergeSort funguje. A vy si ho teď zkuste napsat. Bude to celkem jednoduché - v poli P dostanete čísla k setřídění. Napíšete proceduru MergeSort, které předáte dva parametry - 0 a P.Length. První značí, kde se má začít třídit, a druhý určuje délku úseku, který chcete třídit.
Pokud je délka úseku rovna jedné, procedura může skončit, na úseku délky 1 není totiž co třídit. Pokud je délka úseku rovna dvěma, zkontrolujte, jestli jsou čísla správně seřazená, a pokud ne, prohoďte je. Pokud je úsek delší, pak zavolejte MergeSort na jeho první a druhou polovinu a nakonec spojte oba dva úseky do jednoho tak, jak jsme to dělali v předchozím případě. Je ale třeba jej trochu upravit, hodnoty nebudeme tahat z polí A a B, ale rovnou z našeho velkého pole P, které třídíme. Výsledný setříděný úsek nelze zapisovat rovnou do pole P (přepsali bychom si hodnoty, které budeme potřebovat), takže si jej budeme ukládat do nějakého pomocného pole a po slití pomocné pole do pole P zkopírujeme.
Pokud vám při psaní bude skákat chyba typu StackOverflowException, znamená to, že máte špatně rekurzi. Evidentně správně nepůlíte intervaly a metody MergeSort se volají znova a znova do nekonečna, tak že to .NET framework už nevydrží, protože mu přeteče zásobník. Pamatujte, že když interval rozpůlit nejde, tak se MergeSort už dál volat nesmí!
Mohl by vypadat třeba takto, ale opět doporučuji, abyste si jej zkusili napsat a odladit sami.
Public Sub MergeSort(ByVal start As Integer, ByVal delka As Integer)
If delka = 1 Then 'jeden prvek nemá cenu třídit
Return
ElseIf delka = 2 Then 'podívat se, jestli nejsou hodnoty prohozené
If P(start) > P(start + 1) Then
Dim tmp As Integer = P(start)
P(start) = P(start + 1)
P(start + 1) = tmp
End If
Else 'úsek je delší
Dim start1 As Integer = start 'rozdělit úsek na poloviny
Dim delka1 As Integer = delka / 2
Dim start2 As Integer = start1 + delka1
Dim delka2 As Integer = delka - delka1
MergeSort(start1, delka1) 'setřídit obě poloviny
MergeSort(start2, delka2)
Spojit(start1, delka1, start2, delka2) 'spojit oba úseky
End If
End Sub
Tohle je rekurzivní procedura MergeSort. Většina by měla být jasná, proměnné start1 a start2 určují počátky dvou úseků, proměnné delka1 a delka2 určují jejich délky. Proměnnou delka2 není správné nastavit tako jako delka / 2, protože pokud by náhodou (jako že se to stává) delka bylo liché číslo, třeba 9, pak by délky obou úseků byly 4,5, ale protože jsme v Integeru, zaokrouhlí se obě směrem dolů, tzn. obě délky by byly 4. To ale my nechceme, takže druhou dopočítáme odečtením od celkové délky tříděného úseku.
Public Sub Spojit(ByVal start1, ByVal delka1, ByVal start2, ByVal delka2)
Dim k As Integer = 0 'první ukazatel
Dim l As Integer = 0 'druhý ukazatel
Dim C(delka1 + delka2 - 1) As Integer 'výstupní pole
While k < delka1 Or l < delka2 'opakovat, dokud oba ukazatele nedojely na konec pole
Dim vybrat As Integer
If k = delka1 Then 'už jsme došli na konec prvního pole, takže můžeme tahat jen z druhého
vybrat = 2
ElseIf l = delka2 Then 'už jsme došli na konec druhého pole, takže můžeme tahat jen z prvního
vybrat = 1
Else 'porovnat oba prvky a vybrat menší
If P(start1 + k) < P(start2 + l) Then vybrat = 1 Else vybrat = 2
End If
'opsat vybraný prvek do výstupního pole
If vybrat = 1 Then
C(k + l) = P(start1 + k)
k += 1
Else
C(k + l) = P(start2 + l)
l += 1
End If
End While
'zkopírovat hodnoty z pole C do pole P
For i As Integer = 0 To C.Length - 1
P(start1 + i) = C(i)
Next
End Sub
Toto je nám známá procedura slévání, potřebovala jen pár úprav, aby netahala hodnoty z polí A a B, ale z pole P a v úvahu brala navíc začátek úseku. Na konci je přidané zkopírování setříděného úseku do původního pole P. Pokud byste výsledky ukládali do pole P přímo, tak byste si přepsali hodnoty, které ještě budete potřebovat!
Dim P() As Integer = {12, 93, 3, 0, 45, 17, 29, 41, 10, 53, 54, 50, 49, 6, 67, 81, 11, 27}
Sub Main()
'setřídit pole
MergeSort(0, P.Length)
'vypsat pole
For i As Integer = 0 To P.Length - 1
Console.Write(P(i) & " ")
Next
Console.ReadKey()
End Sub
A toto je hlavní program, pole P je nadeklarováno, takže na něj zavoláme MergeSort a řekneme, že jej chceme setřídit celé. Pak už jej jen vypíšeme.
Tak to byl třídící algoritmus MergeSort, nebylo to až tak složité.
Co je to časová složitost?
Známe tedy už 3 způsoby třídění dat, a již jsem několikrát zmínil, že nejsou všechny stejně dobré. Jak porovnat rychlost těchto algoritmů? Určitě by bylo možné zadat jim milion čísel a nechat je pracovat, přičemž budeme měřit čas, jak dlouho to trvá. To je ale trochu problematické, protože každý počítač je jinak rychlý a záleží na spoustě dalších faktorů. Algoritmy se tedy porovnávají pomocí stanovení časové složitosti. Má to tu výhodu, že navíc třeba víme, že když zdesetinásobíme počet vstupních dat, kolikrát se doba výpočtu prodlouží.
Nás tedy bude zajímat počet kroků, které algoritmus vykoná v závislosti na počtu vstupu. Takovým krokem může být leccos, nemusí to být nutné jeden příkaz, ale třeba jedno prohození dvou hodnot, nebo vnitřek nějakého cyklu, který trvá konstantně dlouho (tzn. ať už je počet vstupních čísel jakýkoliv, ten kousek kódu na něm není závislý, trvá vždy stejně dlouho). Velikost vstupu (počet čísel) budeme označovat N a celou složitost pak budeme zapisovat O(něco). To velké O znamená něco jako horní odhad, zkrátka tak to dopadne, pokud budeme mít ošklivý vstup.
Příklad 1 - složitost vyhledání maxima
Když jsme v poli čísel hledali nejvyšší prvek, programem byl jeden For cyklus, uvnitř něhož byla podmínka. Pokud bylo aktuálně zkoušené číslo větší, uložili jsme ho do nějaké proměnné, jinak se nic nedělalo. Jaká je složitost tohoto programu? Počet čísel v poli je N a pro každé číslo jsme provedli jedno porovnání a přiřazení hodnoty. Jedno samotné porovnání a přiřazení hodnoty trvá vždy stejně dlouho, ať už je čísel sto nebo milion, můžeme to tedy považovat za 1 krok. Takovýchto kroků bude celkem N, pro každé číslo se podmínka provede. Složitost je tedy O(N).
Příklad 2 - algoritmus Select Sort
V minulém díle jsme měli také algoritmus Select Sort. Pokud si nepamatujete, jak funguje, můžete se podívat. V zásadě jsme měli jeden cyklus od 1 do N a v tomto cyklu jsme vždy nalezli minimum a dali jej na správné místo. Vnitřní cyklus tedy měl N kroků, a opakoval se Nkrát, to znamená, že celý algoritmus má složitost O(N.N), tedy O(N2).
Můžete namítnout, že ve skutečnosti vnitřní cyklus neměl vždy N kroků, dokonce v prvním kroku měl N, ve druhém N - 1, ve tředím N - 2, pak N - 3 atd.. až v posledním trval jen 1 krok. To je samozřejmě pravda, můžeme i tuto posloupnost sečíst. 1 + 2 + 3 + ... + N-2 + N-1 + N = N . (N + 1) / 2. Jak se na tohle dá přijít? Jednoduše, stačí si to 1 + ... + N napsat pod to pozpátku. Budeme mít N sloupečků a součat každého bude N + 1, když to vynásobíme, dostaneme součet obou dvou posloupností, my chceme ale jenom jednu, takže to vydělíme dvěma. Když to roznásobíme, máme dohromady N2 + N / 2. Jenomže pro velká N je hodnota N2 tak velká, že nějaké N / 2 můžeme zanedbat.
Obecně vždy do složitosti uvádíme jen tu nejvyšší mocninu N, ostatní hodnoty nás moc nezajímají. I když bychom měli program, který pro 1 číslo udělá vždy právě 1000 kroků (ať už je čísel kolik chce), pořád můžeme napsat, že složitost je O(N), protože pro velká N je 1000.N už skoro stejné a určitě menší než N.N.
Algoritmus Select Sort má tedy časovou složitost O(N2).
Příklad 3 - algoritmus Bubble Sort
Tento algoritmus jsme také měli minule. Jak fungoval? Procházel pole tak dlouho, dokud nacházel nějakou prohozenou dvojici. Pokud by nejnižší číslo bylo až na konci, muselo by zákonitě být přehozeno N-1 krát. Algoritmus tedy celé pole prošel N-1 krát. Vzhledem k tomu, že ostatní čísla mohla být také daleko od své správné pozice, dále než N-1 být už nemohla, takže se v N-1 krocích určitě na správné místo zařadit stihla. Složitost je tedy také O(N2).
Pokud bychom použili vylepšenou verzi, která při přehození zkontroluje, jestli jsme neporušili dvojici předchozí, bude složitost sice lepší, ale také v nejhorším případě ON(N2). Dáme-li totiž algoritmu pole, které je setříděné opačně, poslední prvek bude muset posunout o N-1 míst, předposlední o N-2 atd., takže je to stejné jako u Select Sortu.
Příklad 4 - algoritmus MergeSort
Třídit v čase O(N2) není právě rychlé, příkladem je algoritmus MergeSort, který je rychlejší. Vysvětlit to snad pomůže tento obrázek - jediným místem, kde se něco dělá, je metoda Spojit. Je snadné si rozmyslet, že tato metoda provede tolik kroků, jaká je délka obou úseků. V každém kroku naplní totiž jednu buňku pole C a délka pole C je součet délek obou úseků, které se spojují.
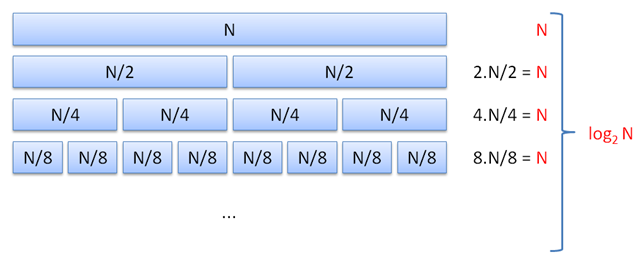
Obrázek je nutné samozřejmě vysvětlit. První zavolání procedury MergeSort na celé pole má složitost N pro spojení dvou úseků + 2 . složitost volání MergeSort na polovinu pole. Každý z nich má složitost N/2 na spojení úseků + 2 . složitost volání MergeSort na čtvrtinu pole atd. Vidíme, že sám první MergeSort udělá N kroků, dva MergeSorty, které zavolal, udělají každý N/2 kroků, ale jsou 2, takže dohromady zase N kroků, podobně i 4 další, pak 8 dalších. Na každé hladině vnoření je tedy složitost N.
Otázkou tedy je, kolik těchto hladin může být. V poslední hladině by bylo N jedniček. Když N vydělíme 2mi, dostaneme počet políček v předposlední hladině. Když to opět vydělíme dvěmi, dostaneme počet polí v předpředposlední hladině atd., až se dostaneme k první hladině s N, kde je už jen jedno pole. Kolikrát se tedy dá N vydělit dvěma? Ptáme se vlastně na toto: když 2k = N, kolik je k? Odpověď je log2 N.
Pokud jste ještě v matematice neměli logaritmy, nevadí. Udělám stručný rychlokurz, co to logaritmus je.
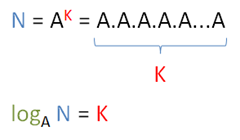
AK (čteme Á na Kátou) je číslo, které dostaneme, když mezi sebou vynásobíme K-krát hodnotu A. Když máme číslo N a chceme zjistit, kolik Aček jsme museli mezi sebou vynásobit (tedy chceme zjistit K), pak to je logA N (čteme logaritmus N o základu A). Například log2 1024 = 10, protože 210 = 1024.
Ale zpět k MergeSortu, my se vlastně ptáme, kolikrát můžeme N vydělit dvěma, tedy kolik dvojek musíme mezi sebou vynásobit, abychom dostali alespoň N (nemusíme se samozřejmě trefit přesně do N, pak nám log vyjde jako desetinné číslo, ale to nás v principu nemusí zajímat). Proto je tedy počet hladin maximálně log2 N, abychom byli přesní, tak to musíme zaokrouhlit nahoru.
Hladin je tedy log2 N a v každé hladině uděláme N kroků, tedy složitost algoritmu je O(N . log N). Je dobré si uvědomit, že funkce log N roste daleko pomaleji než N, složitost N . log N je tedy výrazně lepší než N2. Pokud třeba hodnota N bude milion, tak N2 je 1012 (milion milionů), kdežto log2 1 000 000 ke přibližně 20. Milion milionů a 20 milionů, to je sakra velký rozdíl. Pro setřídění milionu čísel je rozhodně lepší použít MergeSort nebo jiný algoritmus se složitostí O(N.log N).
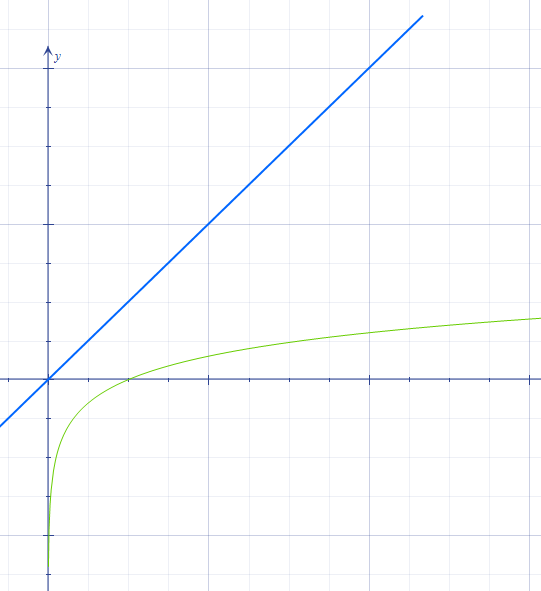
Na tomto obrázku vidíme, jak rychle roste N (modrá) a jak rychle log N (zelená). Už pro hodně malá N je log N výrazně nižší. Na tomto obrázku mají zvýrazněné čtverce rozměry 2 x 2.
Běžné složitosti algoritmů
| O(1) |
konstantní |
| O(log N) |
logaritmická |
| O(N) |
lineární |
| O(N log N) |
lineárně logaritmická |
| O(N2) |
kvadratická |
| O(N3) |
kubická |
| O(2N) |
exponenciální |
Pokud má algoritmus složitost kubickou, ještě se dá použít. Exponenciální složitost je ale prakticky nepoužitelná, už pro N v řádech desítek je hodnota 2N tak vysoká, že by program běžel klidně týdny, měsíce, roky, stovky, tisíce let, miliony let atd. Třeba 232 je něco přes 4 miliardy kroků, na rozdíl od 322, což je 1024 kroků. Existují ale úlohy a problémy, které jinak než exponenciálně řešit neumíme.
Závěrem
V tomto díle jsme si představili třídící algoritmus MergeSort a ukázali jsme si, že je pro velké počty čísel výrazně rychlejší, než SelectSort či BubbleSort. Navíc jsme si ukázali, jak se používá rekurze. V příštím díle si ukážeme algoritmy QuickSort a HeapSort a tím už bude s tříděním konec. Pak se vrhneme na jiné problémy a úlohy.