dotNETportal.cz

Po delší době přichází třetí díl seriálu Naučte se programátorsky myslet, jehož cílem je procvičit si logické uvažování a naučit se základní algoritmy. V minulém díle jsem sliboval mimo jiné algoritmus HeapSort, tak tedy jdeme na něj.

Binární stromy

Malá odbočka do přírodopisu, než začneme s HeapSortem, musíme si vysvětlit, co je to strom.

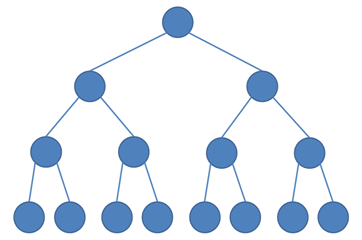
Aby bylo jasno, pokud se bavím o programování, strom je to napravo. To nalevo je můj neumělý pokus o strom, který je možno vidět v přírodě.

Cože to tedy ten strom vlastně je? Je to datová struktura složená z několika vrcholů, kde každý má nejvýše 2 potomky a právě jeden vrchol (kořen) nemá žádného rodiče. To je víceméně definice binárního stromu, pro ternární strom by platilo, že každý vrchol má nejvýše 3 potomky atd. Potomkům někdy říkáme synové.

S binárními stromy se dá dělat spousta krásných věcí a neslouží nám jen k třídění. Jen pro představu – máme například pole, kde je 10000 čísel a chceme v nich nějaké najít. Když jako na potvoru budeme mít smůlu a námi hledané číslo bude až na konci, budeme muset projít celé pole, což není právě dvakrát moudré. Pokud si hodnoty chytře uložíme do stromu, můžeme tím hodně získat.

Binární vyhledávací strom

Speciální typ binárních stromů jsou binární vyhledávací stromy. V každém vrcholu je nějaká hodnota platí vždy, že hodnota v každém vrcholu je větší než hodnoty v levém podstromu, a menší než hodnoty v pravém podstromu. Jako podstrom rozumíme levého resp. pravého syna a všechny jeho potomky.

Pokud bychom chtěli vyhledávat třeba v množině čísel 1, 13, 16, 27, 28, 34, 39, 42, 45, 48, 52, 57, 65, 72, 79, můžeme si strom naplnit hodnotami takto:

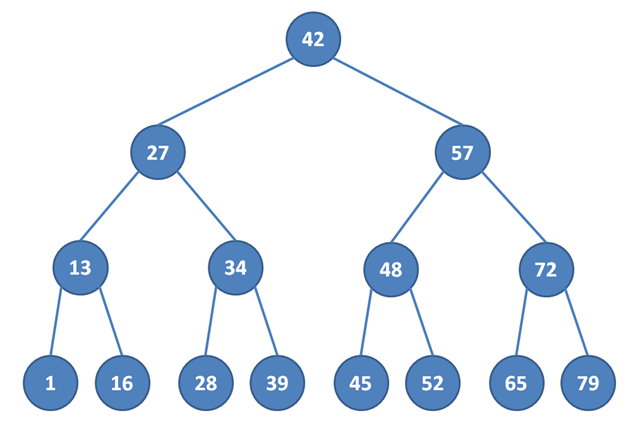
V těchto 15 hodnotách pak můžeme číslo vyhledat na 4 kroky. Zkusme hledat třeba číslo 30. Začneme v kořeni. Víme, že hodnoty v levém podstromu musí být menší než 42, takže číslo 30 bude určitě v levém podstromu. Jdeme tedy do kořene tohoto podstromu, na vrchol 27, a vidíme, že 30 je větší, tudíž musí být napravo. Přejdeme tedy do vrcholu 34 a je jasné, že 30 musí být vlevo. Dostaneme se do 28 a porovnáním zjistíme, že 30 musí být v pravém podstromu. Jenomže vrchol 28 už nemá pravého potomka (nemá ani levého, ale to nás nezajímá), algoritmus končí a odpověď je, že číslo jsme nenašli.

Všimněte si, že pokud hodnoty vypíšete zleva doprava, dostanete je setříděné. To je mimochodem třídící algoritmus TreeSort. Moc se ale v praxi nepoužívá, máme jednodušší.

Vyváženost stromu

Obecně platí, že strom nemusí být takto hezky pravidelný. Zkonstruovat takto “vyvážený strom” (vyvážený znamená, že pro každý vrchol se počet vrcholů v levém a pravém podstromu liší nejvýše o 1) není vždy jednoduché a pokud za běhu do stromu něco přidáváme nebo z něj odebíráme, je to ještě těžší (ale jde to). O tom ale až někdy příště.

Vyváženost stromu hraje dost podstatnou roli pro rychlost operací se stromem, například ono vyhledání hodnoty. Pokud je strom vyvážený, má log N hladin, kde N je počet vrcholů. Pokud je ale strom nevhodně postaven, může mít hladin až N (např. každý vrchol kromě posledního bude mít jen jednoho potomka, což není nijak zakázáno; definice říká, že každý vrchol má nejvýše 2). Pokud by strom nebyl vyvážený měl N hladin, tak bychom si hledání oproti poli vůbec nezjednodušili, ba právě naopak, protože jsme se ještě museli vymýšlet s nějakým stromem.

Proč má vyvážený strom log N hladin? V první hladině je 2⁰ vrcholů (tj. 1), ve druhé 2¹ (tj. 2), ve třetí 2² (tj. 4) atd. Platí, že 2⁰ + 2¹ + … + 2^n-1 = 2ⁿ – 1. Na levé straně rovnice máme počet vrcholů ve vyváženém binárním stromu, který má n hladin, a na pravé straně vidíme, že takový strom má zhruba 2ⁿ vrcholů. Hladin je tedy log₂ N, kde N je počet vrcholů.

Pro milion vrcholů tedy budeme mít asi 20 hladin a umět vyhledat v milionu čísel na 20 kouknutí do stromu, to se již vyplatí. Pro miliardu vrcholů bude hladin asi 30. Potíž bývá opravdu jen s tím takovéto stromy postavit, resp. zajistit u nich vyváženost.

Halda

Proč jsme si o stromech vlastně povídali? Protože v našem algoritmu HeapSort budeme používat datovou strukturu haldu a halda je speciální binární strom. Není to strom vyhledávací, i když se mu trochu podobá. Výhoda je, že se velmi snadno udržuje vyvážená a díky tomu máme zajištěn logaritmický počet hladin vzhledem k počtu vrcholů.

Halda je vyvážený binární strom, kde v každém vrcholu je hodnota nižší než v jeho potomcích. Pokud je navíc poslední hladina nenaplněná, jsou vrcholy naskládány odleva.

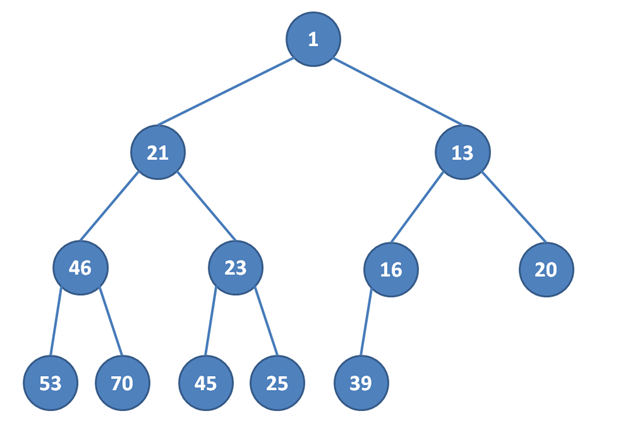
Naše halda může vypadat třeba takto. Je nutné si uvědomit, že na rozdíl od binárního vyhledávacího stromu o vrcholech v haldě kromě kořenu nic moc užitečného nevíme. Všimněme si, že v kořeni haldy je nejnižší hodnota v tomto stromě.

Jak haldu reprezentovat v programu?

Možná si říkáte, jak vůbec takovýhle strom uložit do paměti. Je to, ale v .NETu se u toho většinou neobejdeme bez objektů. Halda se ale dá do paměti uložit jako obyčejné pole. Prostě ji zapíšeme po řádcích do pole a uvědomíme si, že pokud číslujeme od jedničky a jsme v poli na pozici i, tak potomci daného vrcholu jsou na pozicích i * 2 a i * 2 + 1, rodičovský vrchol je pak na pozici i \ 2. Zkuste si to nakreslit, funguje to (vrcholy po řádcích zleva doprava číslujeme od jedničky).

Problém je s tím, že v .NETu se pole standardně číslují od nuly – musíme tedy jedničku před počítáním přičíst a po spočítání zase odečíst. Abychom na to zbytečně nezapomínali, napíšeme si tři jednoduché funkce:

    Public Function Syn1(ByVal i As Integer) As Integer
        Return ((i + 1) * 2) - 1
    End Function

    Public Function Syn2(ByVal i As Integer) As Integer
        Return ((i + 1) * 2)
    End Function

    Public Function Otec(ByVal i As Integer) As Integer
        Return ((i + 1) \ 2) - 1
    End Function

Přidání vrcholu do haldy

Abychom s haldou mohli nějak rozumně pracovat, musíme do ní umět přidat vrchol. Jak to uděláme? Přidáme jej na první volnou pozici. Tím ale můžeme narušit pravidlo, že v každém vrcholu je nižší číslo než v jeho potomcích. Musíme tedy vše pořádně zkontrolovat.

Jak přidávání probíhá je vidět na následujících obrázcích:

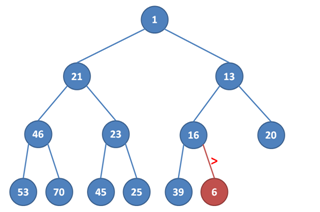
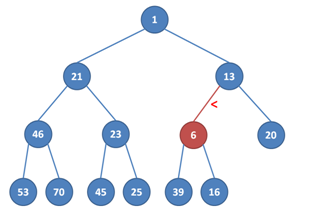
Co jsme přesně udělali?

1. Přidali jsme vrchol na první volnou pozici v poslední hladině. Tím se nám ale porušilo pravidlo, že rodič je menší než syn. Prohodíme hodnotu v nově přidaném vrcholu a v jeho otci.

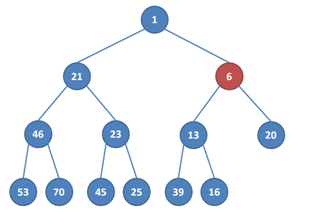
2. Vrcholy 6 a 16 jsme tedy prohodili. Nemohlo se nám rozbít pravidlo u druhého syna červeného vrcholu (vrchol 39), ten byl větší než původní hodnota 16 a je tedy větší než nová hodnota 6, v červeném vrcholu se hodnota zmenšila. Porušilo se nám ale pravidlo s otcem červeného vrcholu, 13 je větší než 6.

3. Abychom to napravili, opět prohodíme, tentokrát vrcholy 13 a 6. Protože 6 je větší než 1, nic se nám nepokazilo a můžeme skončit.

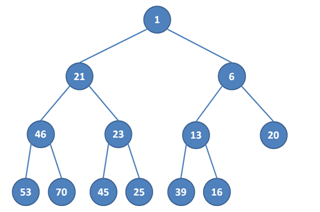
4. Takto vypadá halda po přidání nového vrcholu.

V nejhorším případě se může stát, že takto “probubláme” až do kořene, kde končíme. To by se stalo, kdybychom přidali třeba číslo 0.

Přidání vrcholu do haldy zabere maximálně log N kroků (prohození hodnot ve vrcholech), přesně tolik, kolik máme v haldě hladin.

Cvičení č. 1

Jak už asi tušíte, za úkol budete mít napsat proceduru Pridej, která přidá vrchol do haldy. Můžete použít tuto kostru programu, halda je reprezentována seznamem List(Of Integer), což je takové pěkné nafukovací pole, do nějž můžeme libovolně přidávat vrcholy.

Module Module1

    Dim halda As New List(Of Integer)(New Integer() {1, 21, 13, 46, 23, 16, 20, 53, 70, 45, 25, 39})

    Sub Main()
        Pridat(6)

        Vypis()
        Console.ReadKey()
    End Sub

    Public Sub Pridat(ByVal i As Integer)
        'přidat vrchol na konec haldy a zjistit jeho index
        halda.Add(i)
        Dim index As Integer = halda.Count - 1

        'TODO: sem dopište kód procedury přidání vrcholu

    End Sub

    Public Function Syn1(ByVal i As Integer) As Integer
        Return ((i + 1) * 2) - 1
    End Function

    Public Function Syn2(ByVal i As Integer) As Integer
        Return ((i + 1) * 2)
    End Function

    Public Function Otec(ByVal i As Integer) As Integer
        Return ((i + 1) \ 2) - 1
    End Function

    Public Sub Vypis()
        Dim i As Integer = 0
        Dim delka As Integer = 1
        Dim pos As Integer = 0

        While i < halda.Count
            'výpis hodnoty
            Console.Write("{0} ", halda(i))
            i += 1

            'odřádkování
            pos += 1
            If pos = delka Then     'pokud jsme vypsali celou hladinu, odřádkovat
                Console.WriteLine()
                pos = 0
                delka *= 2      'další řádek bude 2x delší
            End If
        End While
        Console.WriteLine()
    End Sub

End Module

Algoritmus je jednoduchý – po přidání vrcholu do pole jednoduše zkontrolujete, jestli není hodnota v přidaném vrcholu větší než v otci. Pokud ne, tak končíte, pokud ano, tak otce a syna prohodíte a kontrolujete znovu. Pokud dojdete do kořene, končíte také. Ten kořen je dobrý kontrolovat hned na začátku, aby to nepadalo, když budete přidávat do mít prázdné haldy.

Správné přidání vrcholu do haldy by mělo vypadat nějak takto:

    Public Sub Pridat(ByVal i As Integer)
        'přidat vrchol na konec haldy a zjistit jeho index
        halda.Add(i)
        Dim index As Integer = halda.Count - 1

        'kontrola, jestli se neporušilo pravidlo
        While (index > 0) AndAlso (halda(index) < halda(Otec(index)))
            'prohodit
            Dim tmp As Integer = halda(index)
            halda(index) = halda(Otec(index))
            halda(Otec(index)) = tmp

            'kontrolovat o úroveň výš
            index = Otec(index)
        End While
    End Sub

Dokud nejsme v kořeni (to by byl index = 0, kořen haldy je první prvek v poli) a dokud je hodnota v aktuálním vrcholu menší než v rodiči (tedy dokud halda není správná a pravidlo je porušeno), opakujeme jednoduchou věc – prohodíme aktuální vrchol s jeho otcem a aktuální vrchol posuneme o hladinu výš – prostě jej nastavíme na pozici otce.

Všimněte si, že v podmínce cyklu je použit operátor AndAlso – to je specialita Visual Basicu .NET. Pokud bychom použili operátor And, padalo by to při přidávání do prázdné haldy, protože Otec(0) vrátí –1 a v druhé větvi podmínky přistupujeme k této pozici v poli halda, což vyhodí chybu.

Operátor AndAlso provádí tzv. zkrácené vyhodnocování – druhou větev vyhodnocuje jen v případě, že ta první se podařila (pokud selhala, není potřeba ji vyhodnocovat, protože And už stejně nemůže vrátit True). Operátor And naproti tomu vyhodnocuje obě větve vždy. Obdobně máme operátor OrElse, který, pokud první větev platí, už druhou netestuje, protože výsledek je True bez ohledu na to, jestli platí, nebo ne. Or vyhodnotí vždy obě větve podmínky.

V tomto případě jsme tedy použili AndAlso, což zapříčiní, že se druhá větev vyhodnocuje jen tehdy, pokud index > 0 a v takovém případě funkce Otec vrací už hodnoty 0 a vyšší, takže mimo pole sahat nemůžeme.

Jo, možná si říkáte, že je neefektivní volat tolikrát metodu Otec, že ji stačí zavolat jednou a výsledek si někam uložit. Vězte, že tuto optimalizaci za nás udělá kompilátor (pozor, neplatí to vždy, v tomto případě ovšem ano, protože metoda je opravdu velice krátká a navíc nezávisí na ničem jiném než hodnotě svého vstupu).

Odebírání kořene z haldy

Víme již, že halda nám do kořene natlačí vždy nejnižší hodnotu. Co se nám bude při třídění velmi dobře hodit, je zbavení se této nejnižší hodnoty a získání druhé nejnižší atd. To uděláme jednoduše – prostě kořen vyhodíme a haldu jednoduše opravíme, aby to byla zase platná halda. Tak se nám následující minimální hodnota dostane do kořene. Pokud toto provedeme N krát, dostaneme postupně setříděnou posloupnost čísel, tedy to, co jsme chtěli.

Jak na to? Nejmenší prvek nemůžeme jen tak vyhodit, musíme na jeho místo něco dát. Protože budeme chtít haldu zkrátit, ideální by bylo dát tam poslední prvek. Na první místo tedy dáme poslední prvek haldy a haldu hned zkrátíme. Tím se nám ale mohla porušit opět pravidla, což musíme napravit.

Začneme tedy v kořeni a pokud je kořen větší než některý ze dvou synů, vyměníme jej za toho menšího (aby ten druhý byl větší než jeho nový otec a nerozbilo se nám tohle). Takto pokračujeme, dokud nedojdeme na nejnižší úroveň. Je třeba dát pozor na případy, kdy vrchol má jen jednoho syna.

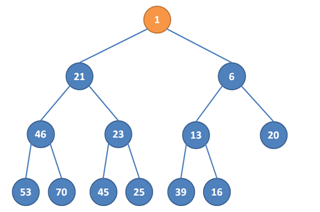
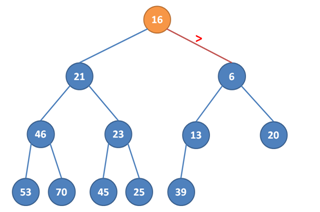
1. Chceme odstranit kořen.

2. Místo kořene tedy dáme poslední prvek a haldu zkrátíme. Tím se nám ale porušila nerovnost, 16 je větší než 6.

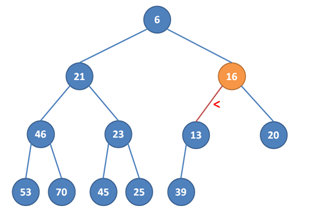
3. Prohodíme tedy 6 a 16, čímž ale máme problém o hladinu níž, protože 13 < 16.

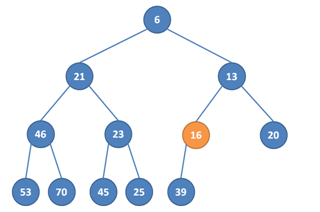
4. Opět tedy provedeme prohození a už je vše v pořádku.

Cvičení č. 2

Zkuste si nyní napsat metodu OdebratKoren, která celý tento postup provede. Není na tom nic těžkého. Můžete opět vyjít z této kostry:

    Public Function OdebratKoren()
        'přesunout poslední vrchol do kořene
        If halda.Count = 0 Then Throw New InvalidOperationException()
        OdebratKoren = halda(0)     'nastavit návratovou hodnotu
        halda(0) = halda(halda.Count - 1)
        halda.RemoveAt(halda.Count - 1)
        Dim index As Integer = 0

        'TODO: sem dopsat kód procedury odebrání kořene

 
    End Function

Není na tom opět nic složitého. Bude tam cyklus, který poběží, dokud má vrchol ještě nějaké syny (index vrcholů, které jsou ještě v haldě je ostře menší než halda.Count, číslují se totiž od nuly). V každém kroku se vybere ten ze synů, který má nižší hodnotu (pozor i na případy, kdy má vrchol jen levého syna a pravého ne, to je třeba konkrétně oranžový vrchol na posledním obrázku). Pokud je hodnota v menším synovi menší než v aktuálním vrcholu, je třeba tyto dva prohodit a pokračovat dál o hladinu níž. Pokud je otec menší než menší ze synů, pak je již vše v pořádku a musíme z cyklu vyskočit příkazem Exit While.

Jak to má vypadat správně?

    Public Function OdebratKoren()
        'přesunout poslední vrchol do kořene
        If halda.Count = 0 Then Throw New InvalidOperationException()
        OdebratKoren = halda(0)     'nastavit návratovou hodnotu
        halda(0) = halda(halda.Count - 1)
        halda.RemoveAt(halda.Count - 1)
        Dim index As Integer = 0

        'opravit pravidlo, pokud je porušeno
        While (Syn1(index) < halda.Count)       'dokud má vrchol alespoň 1 syna
            'zjistit, který ze synů má menší hodnotu
            Dim mensiSyn As Integer = Syn1(index)
            If Syn2(index) < halda.Count AndAlso halda(Syn2(index)) < halda(Syn1(index)) Then mensiSyn = Syn2(index)

            'pokud je hodnota menší než v aktuálním vrcholu, prohodit, jinak končíme
            If halda(index) > halda(mensiSyn) Then
                Dim tmp As Integer = halda(index)
                halda(index) = halda(mensiSyn)
                halda(mensiSyn) = tmp

                'kontrolovat o úroveň níž
                index = mensiSyn
            Else
                'končíme
                Exit While
            End If
        End While
    End Function

Pokud se vám algoritmus nepodařilo vymyslet, doporučuji zkusit si to nakreslit a pak to napsat ještě jednou. Není to opravdu nic složitého, chce si to jen hrát. Klidně si vystříhejte z papíru čísla s šoupejte si s nimi po papíře, pokud nechápete dokonale princip, nemá smysl dále číst.

Podotýkám, že odebrání kořene zabere, stejně jako přidávání, maximálně log N kroků.

Jak funguje HeapSort?

Jak tedy třídit pomocí haldy? Velmi jednoduše. Prostě všechny tříděné prvky nejprve vložíte do haldy a pak budete odebírat kořen tak dlouho, dokud celou haldu nevyprázdníme. Možná to vypadá strašně složitě a divně, ale je to rychlejší než bublinkové třídění nebo třídění výběrem z prvního dílu, složitost je totiž opět O(N log N). Přidání či odebrání jednoho prvku zabere čas log N a každou činnost děláme pro každý prvek, kterých je N právě jednou.

Celý algoritmus může vypadat třeba takto:

Module Module1

    Dim halda As New List(Of Integer)
    Dim pole() As Integer = New Integer() {12, 1, 3, 16, 84, 23, 56, 0, 5, 19, 27, 44, 15}

    Sub Main()
        HeapSort()
        VypisPole()
        Console.ReadKey()
    End Sub

    Public Sub HeapSort()
        'naházet všechny prvky na haldu
        For i As Integer = 0 To pole.Length - 1
            Pridat(pole(i))
        Next
        'vytahat setříděně prvky z haldy
        For i As Integer = 0 To pole.Length - 1
            pole(i) = OdebratKoren()
        Next
    End Sub

    Public Sub VypisPole()
        'vypsat pole 
        For i As Integer = 0 To pole.Length - 1
            Console.Write("{0} ", pole(i))
        Next
        Console.WriteLine()
    End Sub

    Public Sub Pridat(ByVal i As Integer)
        'přidat vrchol na konec haldy a zjistit jeho index
        halda.Add(i)
        Dim index As Integer = halda.Count - 1

        'kontrola, jestli se neporušilo pravidlo
        While (index > 0) AndAlso (halda(index) < halda(Otec(index)))
            'prohodit
            Dim tmp As Integer = halda(index)
            halda(index) = halda(Otec(index))
            halda(Otec(index)) = tmp

            'kontrolovat o úroveň výš
            index = Otec(index)
        End While
    End Sub

    Public Function OdebratKoren()
        'přesunout poslední vrchol do kořene
        If halda.Count = 0 Then Throw New InvalidOperationException()
        OdebratKoren = halda(0)     'nastavit návratovou hodnotu
        halda(0) = halda(halda.Count - 1)
        halda.RemoveAt(halda.Count - 1)
        Dim index As Integer = 0

        'opravit pravidlo, pokud je porušeno
        While (Syn1(index) < halda.Count)       'dokud má vrchol alespoň 1 syna
            'zjistit, který ze synů má menší hodnotu
            Dim mensiSyn As Integer = Syn1(index)
            If Syn2(index) < halda.Count AndAlso halda(Syn2(index)) < halda(Syn1(index)) Then mensiSyn = Syn2(index)

            'pokud je hodnota menší než v aktuálním vrcholu, prohodit, jinak končíme
            If halda(index) > halda(mensiSyn) Then
                Dim tmp As Integer = halda(index)
                halda(index) = halda(mensiSyn)
                halda(mensiSyn) = tmp

                'kontrolovat o úroveň níž
                index = mensiSyn
            Else
                'končíme
                Exit While
            End If
        End While
    End Function

    Public Function Syn1(ByVal i As Integer) As Integer
        Return ((i + 1) * 2) - 1
    End Function

    Public Function Syn2(ByVal i As Integer) As Integer
        Return ((i + 1) * 2)
    End Function

    Public Function Otec(ByVal i As Integer) As Integer
        Return ((i + 1) \ 2) - 1
    End Function

    Public Sub Vypis()
        Dim i As Integer = 0
        Dim delka As Integer = 1
        Dim pos As Integer = 0

        While i < halda.Count
            'výpis hodnoty
            Console.Write("{0} ", halda(i))
            i += 1

            'odřádkování
            pos += 1
            If pos = delka Then     'pokud jsme vypsali celou hladinu, odřádkovat
                Console.WriteLine()
                pos = 0
                delka *= 2      'další řádek bude 2x delší
            End If
        End While
        Console.WriteLine()
    End Sub

End Module

Jak je vidět, samotný HeapSort je triviální, pokud máme hotovou a napsanou haldu.

Cvičení č. 3

Celé se to dá ještě trochu zoptimalizovat, například nepotřebujeme k tomu mít haldu zvlášť. Vaším úkolem je teď celý program upravit tak, aby nepoužíval proměnnou halda, ale všechno setřídil v rámci jednoho pole, halda i prvky, se kterými pracujeme, bude v poli pole (nemusíte ho dělat delší než je počet prvků).

Rada je následující – na začátku má halda velikost 0 a seznam čísel k setřídění začíná od nuly. Jakmile vezmu první prvek a přidám jej do haldy, délka haldy se zvětší na 1 a pole čísel, které jsem ještě nenačetl, bude začínat od jedničky. Načtením dalších čísel se bude halda zvětšovat a ukrajovat ze seznamu čísel místa, která již nepotřebujeme. Zkrátka halda bude normálně v poli pole, akorát pro její velikost si musíme udělat speciální proměnnou, nemáme už totiž halda.Count a délku pole použít nemůžeme, to je pořád stejně dlouhé.

Při odebírání prvků z haldy se nám zase bude halda zkracovat a tím nám v poli pole budou vznikat položky, které halda již nepoužije a které můžeme použít k uložení výsledku. Jediný problém je v tom, že odebráním prvního prvku se nám uvolní poslední položka v poli, tam tedy prvek uložíme. Jakmile zničíme celou haldu, budeme mít posloupnost v poli setříděnou, ale pozpátku. Takže nakonec zbývá ještě výstupní pole otočit pozpátku, ale to už by měla být hračka.

Závěrem

Pokud máte nějaké připomínky či náměty, určitě je napište do diskuse. Na QuickSort dnes již nedojde, ale to nám nevadí, protože se na něj podíváme příště.